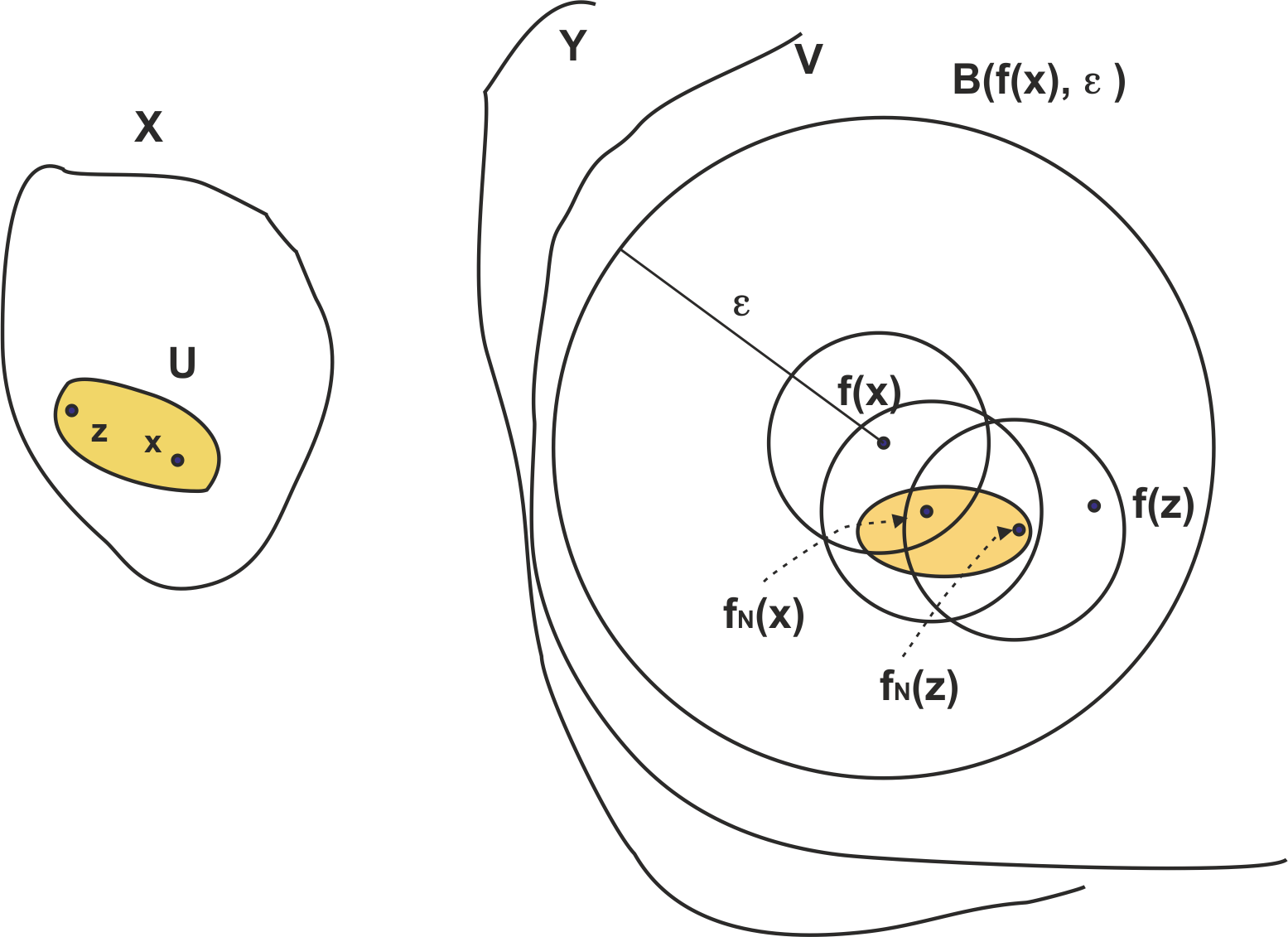
Convergencia uniforme

Proposición. Si la sucesión de aplicaciones $f_n: X \to Y$, converge uniformemente a $\, f: X \to Y$, entonces $f$ es continua.

Demostración. Vamos a demostrar que $f$ es continua en cada punto $x \in X$. En efecto, Sea $V$ un entorno abierto de $f(x)$. Existe una bola, $B(f(x), \varepsilon) \subset V$.

Por la convergencia uniforme, existe un índice $N$ tal que, si $n \geq N$, $\,d(f_n(z), f(z)) < \frac{\varepsilon}{3})$, para todo $z \in X$.

Por la continuidad de $f_N$, existe un entorno abierto $U$ de $x$ tal que $f_N(U) \subset B(f_N(x), \frac{\varepsilon}{3})$.

Por tanto, para todo $z \in U$, $$ d\left( f(z), f(x)\right) \leq d\left( f(z), f_N(z)\right) + d\left( f_N(z), f_N(x)\right) + d\left( f_N(x), f(x)\right) < \varepsilon $$ Es decir, $\, f(U) \subset B(f(x), \varepsilon) \subset V$.