Grupos de homotopía

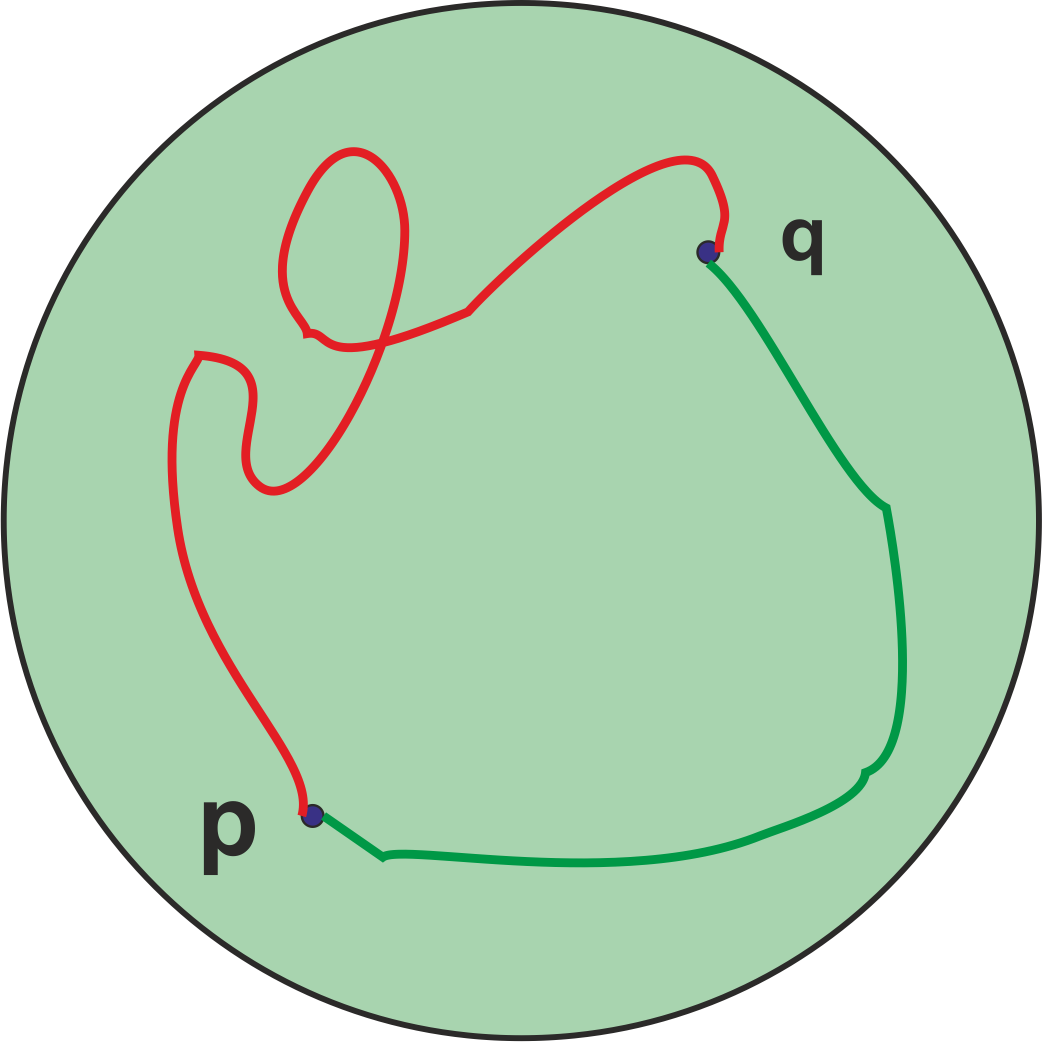
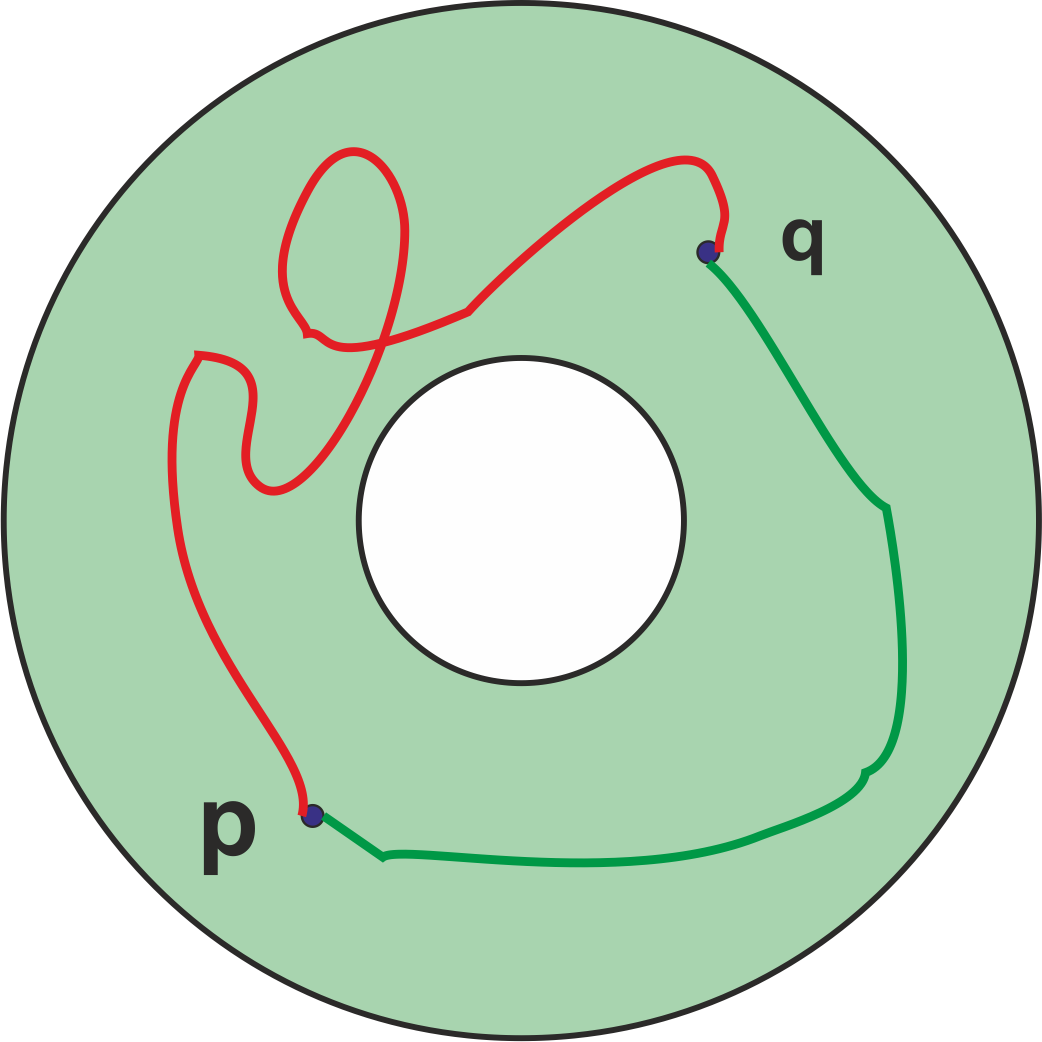
Hemos definido la arco-conexidad como la posibilidad de ir de un punto a otro del espacio por un camino continuo. En general habrá muchos caminos que nos lleven de un punto al otro. Consideremos por ejemplo un disco y una corona circular en el plano.

Los dos espacios son arco-conexos pero hay una diferencia importante entre ellos. En el caso de la corona circular hay dos maneras que apreciamos como diferentes para unir por un camino los puntos $p$ y $q$. En el caso del disco, todas las formas las podemos considerar como equivalentes. Vamos a tratar de precisar este hecho.

Observemos primero que la diferencia esencial entre el disco y la corona es que esta tiene un agujero: los dos caminos diferentes pasan a uno y otro lado del agujero. Si imaginamos una cuerda que sigue uno de los caminos no podemos deformarla para que coincida con el otro camino sin salirnos de la corona. En el caso del disco, cualquier par de caminos que una los puntos pueden deformarse el uno en el otro sin salirnos del disco.

Cuando hemos hablado de caminos equivalentes estábamos pensando en caminos que se pueden deformar uno en otro. En Matemáticas se dice que estos caminos son homótopos. Solo tenemos pues que dar una definición matemática de este concepto.

Sea $X$ un espacio y sean $$ \omega: [0, 1] \longrightarrow X, \qquad \rho: [0,1] \longrightarrow X $$ dos caminos con origen $p=\omega(0) = \rho(0)$ y final $q=\omega(1)=\rho(1)$. (Por camino entendemos una aplicación continua.) Diremos que los dos caminos son homótopos si existe una aplicación continua $$ H: [0,1] \times [0, 1] \longrightarrow X $$ tal que
1. Fijando la segunda componente se obtienen caminos contínuos $$ H_s: [0,1] \longrightarrow X, \qquad H_s(t) = H(t,s) $$ todos con origen en $p$ y final en $q$: $H_s(0) = p$ y $H_s(1)=q$.
2. Los caminos $H_0$ y $H_1$ coinciden con $\omega$ y $\rho$, respectivamente: $H_0 = \omega$, $H_1 = \rho$.

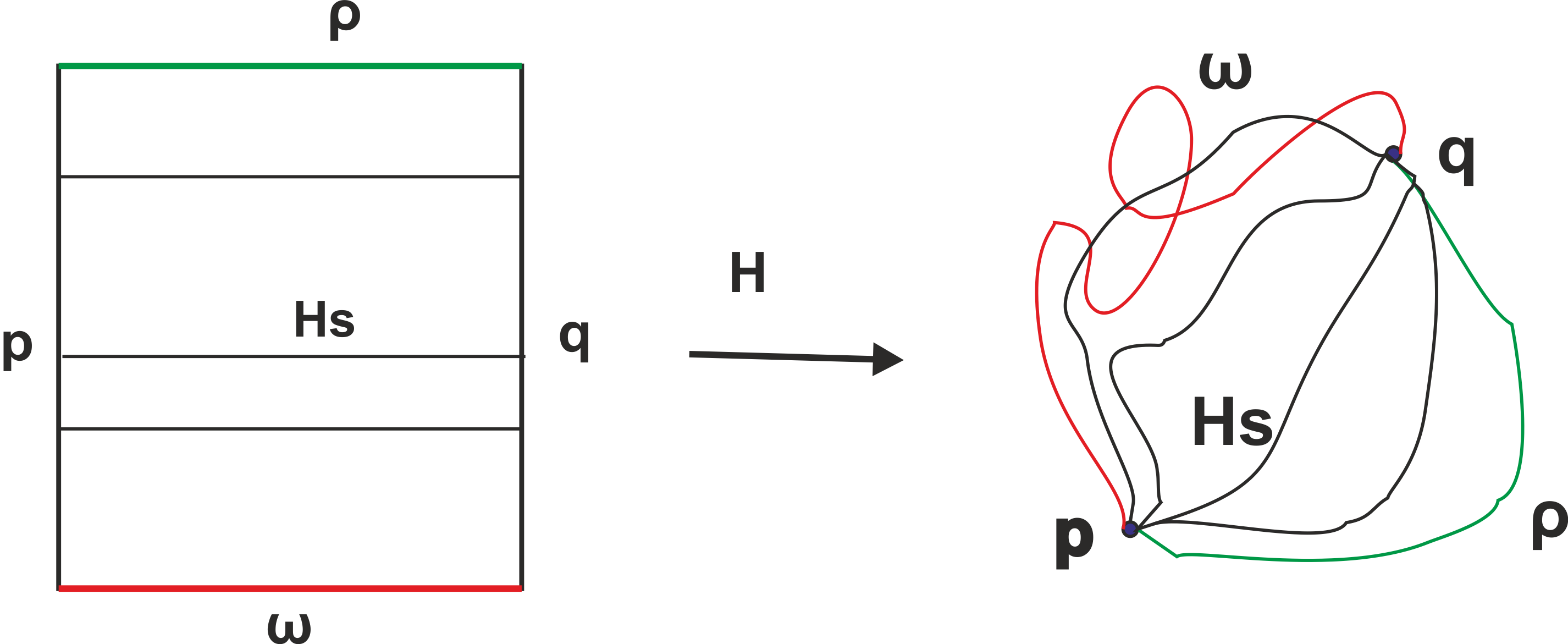
La aplicación $H$ se llama una homotopía de $\omega$ en $\rho$ y es la traducción matemática de la idea de un conjunto de caminos, $H_s$, que pasen de forma continua de un camino $\omega$ a un camino $\rho$. Podemos decir pues que $H$ es un camino de caminos $H_s$, $s \in [0, 1]$, que une los caminos $\omega$ y $\rho$. Por tanto la situación es similar a la de un camino ordinario $\omega$, que es una serie de puntos $\omega(s)$, $s \in [0, 1]$, que pasan de forma continua de un punto $\omega(0)$ a un punto $\omega(1)$.

Observación: Es útil imaginar que la variable $t$ es el tiempo. Entonces todos los caminos los hemos supuesto recorridos en el mismo tiempo, lo cual es cómodo para las demostraciones matemáticas. Naturalmente, los caminos con un recorrido más largo se recorreran a mayor velocidad. En relación con la homotopía esto no tiene mucha importancia. Es fácil ver que un camino es homótopo a cualquier camino con el mismo recorrido y velocidades distintas en cada punto (o incluso nula), siempre que el tiempo total en que se recorre sea $1$.

A veces es útil imaginar el recorrido del camino como un cordel. Al hacer una homotopía $H$ los recorridos de los caminos $H_s$ son deformaciones del recorrido inicial. Ahora bien, el recorrido de los caminos $H_s$ pueden ser más largos o más cortos que el de partida. Por eso, más que en un cordel, deberíamos hablar de una goma elástica. Aunque esta tiende a encogerse a la menor longitud posible y tampoco sería una buena imagen. Así pues, nos referiremos a cordeles pero entendiendo que se pueden encoger o estirar según la longitud de los $H_s$.

Al igual que las componentes arco-conexas son los subconjuntos de puntos que pueden unirse unos con otros por un camino, podemos agrupar los caminos en conjuntos de caminos homótopos. Pero hay diferencias importantes: la primera es que la homotopía solo compara caminos con el mismo origen y final.

Lo que haremos es tomar solo caminos cerrados, es decir caminos en que su origen coincide con su final. Todos los caminos $H_s$ intermedios de una homotopía entre caminos cerrados, son caminos cerrados con el mismo origen y el mismo final. Este origen y final se llama punto base del camino.

Los caminos cerrados sirven también para detectar el agujero de una corona circular. Fijado un punto $p$ de la corona, el camino constante en $p$ y el camino que rodea el agujero y vuelve a $p$ no son equivalentes, esto es, no son homótopos. En cambio en un disco todos los caminos cerrados con el mismo punto base son homótopos entre ellos y homótopos al camino constante, que no se mueve del punto base.

Consideremos pues, todos los caminos cerrados de un espacio $X$, con origen y final en un punto $p \in X$; lo designaremos por $C(X, p)$. Consideremos los subconjuntos maximales de $C(X, p)$ formados por caminos homótopos entre sí. Obtenemos así una serie de conjuntos disjuntos cuya unión es $C(X, p)$ (necesita una demostración).

Veamos un ejemplo. Sea $CoCir$ una corona circular del plano y $p$ un punto de la misma. La aplicación constante en $p$ es un camino. La aplicación que da una vuelta al agujero central y vuelve a $p$ es otro camino; también la que da $n$ vueltas en uno u otro sentido. Escribamos ecuaciones. Sea $$ p = (\frac12, 0) \quad \in \quad CoCir = \{ (x,y) \in \mathbb R^2 \mid \frac12 \leq \sqrt{x^2 + y^2} \leq 1 \} $$ y consideramos el camino $ \nu_n: [0,1] \longrightarrow CoCir$: $$ \nu_n (t) = \frac12 \left( \cos(2\pi n t), \sin(2\pi n t) \right), \qquad t \in [0, 1] $$ que da $|n|$ vueltas en el sentido opuesto a las agujas del reloj si $n > 0$, y en el sentido de las agujas del reloj si $n < 0$. Para $n = 0$ se trata del camino constante.

Cualquier camino de $CoCir$ con punto base $p$ es homótopo a uno de los caminos $\nu_n$. Nos será fácil convencernos de que es lógico que sea así considerando un cordel que recorre un camino arbitrario. Imaginemos que estiramos de un punto muy cercano al final. Las posiciones que va tomando el cordel son caminos cerrados que varían de forma continua. Estirando suficientemente, el cordel acabará enrollado en el borde interior de la corona (encogido a una longitud más corta que la inicial probablemente). El camino final es uno de los $\nu_n$. También es fácil convencerse que los caminos $\nu_n$ no son homótopos entre sí. Naturalmente, por mucho que nos sea fácil imaginar que esto realmente funciona así, es necesario hacer las demostraciones. Nosotros las omitimos de nuevo.

Designemos por $\pi(X, p)$ al conjunto de subconjuntos maximales de $C(X, p)$ formados por caminos homótopos entre sí. En el caso de la corona circular $CoCir$ este conjunto está en correspondencia biyectiva con los enteros: $\; \nu_n \mapsto n$.

Vamos a definir una operación en $\pi(X, p)$ que llamaremos producto. Una operación es un criterio por el que a cada par de elementos le asignamos otro elemento. Es decir, es una aplicación $$ \pi(X, p) \times \pi(X, p) \longrightarrow \pi(X, p) $$ ¿Cómo lo hacemos? Tomemos dos elementos de $\pi(X, p)$, es decir, dos conjuntos de caminos, y escojamos un camino de cada conjunto: $\omega$ y $\rho$. Los elementos son pues el conjunto de todos los caminos homótopos a $\omega$ y el conjunto de todos los caminos homótopos a $\rho$. Los designaremos por $[\omega]$ y $[\rho]$ y se llaman las clases de $\omega$ y $\rho$ respectivamente. Diremos que $\omega$ es un representante de la clase $[\omega]$, y que $\rho$ es un representante de la clase $[\rho]$. Definimos un camino cerrado tal que, para todo $t \in [0, 1]$, $$ \omega\cdot\rho = \left\{ \begin{array}{lcl} \omega(2t) & \text{si} & 0 \leq t \leq 1/2 \\ \rho(2t-1) & \text{si} & 1/2 \leq t \leq 1 \end{array} \right. $$ $\omega\cdot\rho$ es un camino que recorre $\omega$ y después $\rho$. Se llama la composición de $\omega$ y $\rho$.

El resultado de operar $[\omega]$ y $[\rho]$ es la clase de representante $[\omega\cdot\rho]$: $$ [\omega] \cdot [\rho] = [\omega\cdot\rho] $$

Muy importante: Para que esto sea una definición matemática correcta necesitamos demostrar que el resultado no depende de los representantes que hayamos tomado. Es decir, que al componer caminos homótopos se obtienen caminos homótopos: $$ [\omega'] = [\omega], \; [\rho'] = [\rho] \quad \Rightarrow \quad [\omega\cdot\rho ] = [\omega'\cdot\rho'] $$

El conjunto $\pi(X, p)$ junto con la operación que acabamos de definir, se llama grupo fundamental del espacio $X$, con punto base $p$.

La definición general de grupo es la siguiente:

En matemáticas se llama se llama grupo a un conjunto $G$, provisto de una operación $G \times G \to G$, que aplica a designar por $g_1 \cdot g_2$, y llamar producto de $g_1$ y $g_2$ (aunque puede tener otros nombres y otra manera de designarlo). La operación debe cumplir las siguientes propiedades:
1. Existe un elemento, que llamaremos unidad y designaremos por $1$, que cumple $$ g \cdot 1 = g = 1 \cdot g, \qquad \text{para todo} \; g \in G $$ 2. Propiedad asociativa: Para cualquier terna de elementos $g_1, g_2, g_3 \in G$: $$ g_1 \cdot (g_2\cdot g_3) = (g_1 \cdot g_2) \cdot g_3 $$ 3. Para todo $g \in G$, existe un elemento, que llamaremos inverso de $g$, y designaremos por $g^{-1}$, que cumple $$ g \cdot g^{-1} = 1 = g^{-1}\cdot g $$

La operación que hemos definido en $\pi(X, p)$ cumple estas tres propiedades. El elemento $1$ es la clase del camino constantemente el punto base. El inverso de la clase del camino $\omega$ es la clase del camino $\omega^{-1}$ que recorre los mismos puntos que $\omega$ en sentido inverso: $\omega^{-1}(t) = \omega(1-t)$.

Los enteros $\mathbb Z$ y los reales $\mathbb R$, con la suma forman un grupo; su elemento "unidad" es $0$ y se llama cero (no uno) (por eso a lo que hemos llamado unidad se le llama generalmente elemento neutro: cualquier elemento operado con él no cambia). Si consideramos $\mathbb Z$ con el producto no es un grupo porque la mayoría de sus elementos no tienen inverso. Tampoco lo es $\mathbb R$ con el producto. En este caso sí que los elementos tienen inverso, todos menos el $0$. Si quitamos este cero, $\mathbb R \setminus 0$ con el producto sí es un grupo.

En el caso de la corona circular tenemos una aplicación uno-a-uno (biyectiva) $$ \pi(CoCir, p) \to \mathbb Z $$ que aplica una clase $[\nu_n]$ en $n$ y aplica el producto de dos clases en la suma de sus imágenes: la composición del camino que da $n$ vueltas y el camino que da $m$ vueltas es un camino que da $n+m$ vueltas: $ \nu_n\cdot\nu_m =\nu_{n+m}.$ Es decir, pensando solo en la operación, es como si $\pi(CoCir, p)$ tuviera como elementos los enteros (con otro nombre), y la operación fuera la suma de esos enteros. En particular, $\nu_n^{-1} = \nu_{-n}$.

Dos grupos, sean $G$ y $H$, son isomorfos si existe una aplicación biyectiva entre ellos, $f: G \to H$ que conserva las operaciones, es decir para todo par de elementos $x, y \in G$, la imagen de un producto es el producto de imágenes: $$ f(x \cdot y) = f(x)\cdot f(y) $$

Los grupos $\pi(CoCir, p)$ y $\mathbb Z$ (con la suma) son isomorfos. Nos referiremos a este hecho diciendo simplemente que el grupo fundamental de $CoCir$ es $\mathbb Z$.

Importancia del punto base. El grupo $\pi(X, p)$ que acabamos de definir no solo depende del espacio $X$ sino que también depende del punto $p$. Se puede demostrar que este grupo es el mismo siempre que $p$ se conserve en la misma arco-componente conexa. Concretamente, si $\tau: [0,1] \to X$ es un camino con origen $q=\tau(0)$ y final $p=\tau(1)$, podemos definir una aplicación

$$ \psi_\tau: \pi(X, p) \longrightarrow \pi(X, q), \qquad \psi_\tau \left([\omega]\right) = [\tau\cdot \omega \cdot \tau^{-1}] $$ donde $\tau^{-1}(t) = \tau(1-t)$ es el camino que recorre los mismos puntos que $\tau$ en sentido inverso. Se puede demostrar que la aplicación $\psi_\tau$ está bien definida en el sentido de que la imagen de $[\omega]$ no depende del representante que tomemos: $$ \omega' \in [\omega] \quad \Rightarrow \quad [\tau^{-1}\cdot \omega' \cdot \tau] = [\tau^{-1}\cdot \omega \cdot \tau] $$

Análogamente, la aplicación $$ \psi_{\tau^{-1}}: \pi(X, q) \longrightarrow \pi(X, p), \qquad \psi_{\tau^{-1}} \left([\rho]\right) = [\tau^{-1}\cdot \rho \cdot \tau] $$ está bien definida y las composiciones $\psi_\tau\circ\psi_{\tau^{-1}}$ y $\psi_{\tau^{-1}}\circ\psi_{\tau}$ son la identidad. Por tanto, las dos aplicaciones son biyectivas. Además se puede demostrar también que $\psi_\tau$ (y $\psi_{\tau^{-1}}$ ) conservan la operación: la imagen de un producto es igual al producto de imágenes $$ \psi_\tau ([\omega]\cdot[\omega'])=\psi_\tau([\omega])\cdot \psi_\tau([\omega']) $$ Ambas aplicaciones son isomorfismos. Así pues, si el espacio es arco-conexo podemos tomar como punto base el que más nos convenga. Si el espacio tiene varias componentes conexas, los grupos fundamentales de unas u otras pueden ser muy diferentes.