Productos infinitos

En el caso del producto de una familia infinita de espacios topológicos, las uniones de productos de un abierto de cada uno de los espacios forman también una topología que se llama topología de cajas. Ahora bien, esta topología tienen muchos inconvenientes en el caso infinito. $\, f: Y \longrightarrow \prod_{j\in J} X_j\, $ puede no ser continua aunque todas las composiciones con las proyecciones sean todas. Damos un ejemplo.

Ejemplo

Consideremos el producto de una infinidad numerable de copias de $\mathbb R$ y la aplicación $$ f: \mathbb R \longrightarrow \prod_{j \in \mathbb N} \mathbb R, \qquad f(t) = (t, t, t, \dots ) $$ Las composiciones con las proyecciones son la identidad y, en particular, continuas. Si dotamos al producto con la topología de cajas, que tiene como abiertos los productos de un abierto de cada componente, $f$ no es continua. En efecto, con esta topología $\, U = \prod_{j \in \mathbb N} (-\frac{1}{j}, + \frac{1}{j})\,$ es un abierto que contiene $f(0)$. Ahora bien, cualquier entorno de $0 \in \mathbb R$ contiene un intervalo $\, (- \varepsilon, \, \varepsilon)$, con $\varepsilon >0$ suficientemente pequeño. Para $j$ suficientemente grande $$ \frac{1}{j} < \frac{\varepsilon}{2} \quad \Rightarrow\quad (- \varepsilon, \, \varepsilon) \not\subset (-\frac{1}{j}, + \frac{1}{j}) \quad\Rightarrow \quad f(- \varepsilon, \, \varepsilon) \not\subset U $$ Lo que demuestra que $f$ no es continua.

Para definir una topología en el producto cartesiano de espacios topológicos, se considera prioritario que la continuidad de las composiciones con las proyecciones asegure la continuidad de $f$. En la demostración de esta propiedad para el caso finito (aquí) se explica por qué la demostración no funciona para el caso infinito: tomar productos de un abierto de cada espacio es tomar demasiados abiertos. La solución es tomar solo los imprenscindibles para que las proyecciones sean continuas.

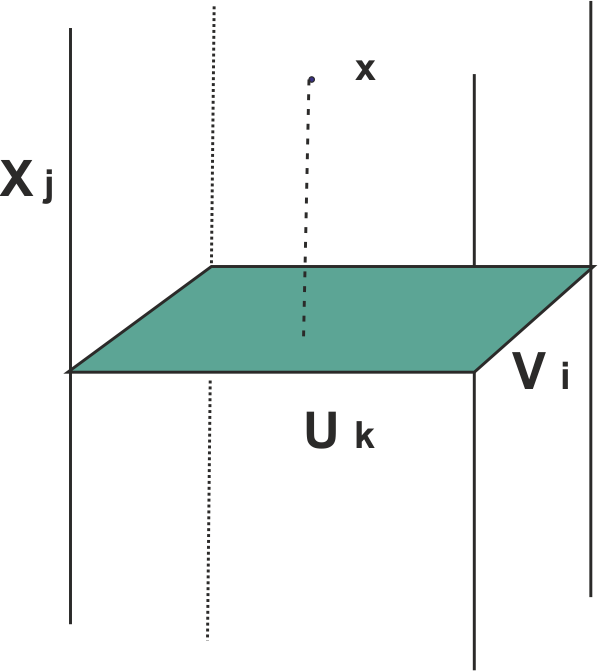
Sea $\left\{ (X_j, \tau_j) \mid j\in J \right\}$ una familia de espacios topológicos. Las antiimágenes de un subconjunto $A$ del producto por la proyección $k$-ésima es el conjunto de puntos que tienen la coordenada $k$-ésima en $A$: $$ p_k : \prod_j X_j \longrightarrow X_k, \quad \qquad p_k^{-1}(A) = \{ (x_j)_{j\in J} \mid x_k \in A \}, \qquad A \subset X_k $$ La continuidad de $p_k$ implica que, para cualquier abierto $U_k$ de $X_k$, $$ p_k^{-1}(U_k) = \{ (x_j)_j \in \prod_j X_j \mid x_k \in U_k \} $$ sea abierto. Ahora bien, si estos conjuntos son abiertos, también lo tienen que ser sus intersecciones finitas. Es decir, para todo conjunto finito de abiertos $U_{k_1} \in \tau_{k_1}$, ... , $U_{k_m} \in \tau_{k_m}$, el conjunto $$ p_{k_1}^{-1}(U_{k_1}) \cap \dots \cap p_{k_m}^{-1}(U_{k_m}) = \{ (x_j)_{j\in J} \mid x_{k_1} \in U_{k_1}, \dots, x_{k_m} \in U_{k_m} \} $$ tiene que ser abierto de $X$. Podemos simplificar la notación designando este conjunto por $$ U_{k_1} \times \dots \times U_{k_m} := p_{k_1}^{-1}(U_{k_1}) \cap \dots \cap p_{k_m}^{-1}(U_{k_m}) $$

Dada una familia arbitraria $(X_j, \tau_j)$, $\, j\in J$, de espacios topológicos, se llama espacio producto al conjunto producto $X=\prod X_j$ con la topología que tiene como abiertos todos los conjuntos $U_{k_1} \times \dots \times U_{k_m} $, para cualquier familia finita de índices, $ \{ k_1, \dots, k_m \} \subset J$, y cualquier elección de abiertos $U_{k_i} \subset X_{k_i}$; y por las uniones arbitrarias de este tipo de subconjuntos.

Observemos que las coordenadas de índices $j$ que no aparecen en $\,U_{k_1} \times \dots \times U_{k_m}\,$ varían libremente en todo el espacio $X_j$. Es decir, si el producto es infinito, los abiertos son todos "muy grandes".

Con esta definición el producto infinito cumple las mismas propiedades que demostramos para el caso finito.

Proposición.
1. Las proyecciones $p_k: \prod_{j\in J} X_j \to X_k$, definidas por $\, p_k(x_j) = x_k$, son continuas.

2. Una aplicación $f: Y \to \prod_{j\in J} $ de un espacio topológico $(Y, \rho)$ en un espacio producto, es continua si, y solo si, todas las aplicaciones $$ f_k: Y \stackrel{f}{\longrightarrow} \prod_{j\in J} X_j \stackrel{p_k}{\longrightarrow} X_k $$ son continuas.

Demostración.

Proposición. Las proyecciones son abiertas, es decir, transforman abiertos en abiertos.

Demostración.