Propiedades de separación

En un espacio topológico, los entornos de un punto miden, en cierta manera, el grado de proximidad del resto de puntos, de forma análoga a como lo hacen las bolas en un espacio métrico. Las propiedades de separación se refieren a la existencia de entornos disjuntos: cierto grado de proximidad a un punto impide mayor proximidad a otro punto.

Diremos que un espacio topológico $(X, \tau)$ es Hausdorff , o $T_2$, si dos puntos distintos tienen siempre entornos disjuntos.

Ejemplo

Los espacios métricos son de Hausdorff ya que, si dos puntos $x,y$ son distintos, su distancia no es cero y las bolas con centro en estos puntos y radio $r \leq \frac{d(x,y)}{2}$ son disjuntas.

En particular, en un espacio de Hausdorff, ninguna sucesión puede estar, a partir de un índice, en los dos entornos. Es decir cualquier sucesión tiene, como máximo, un límite.

La propiedad siguiente da una caracterización de los espacios Hausdorff que resulta, a menudo, muy útil. Un ejemplo es el corolario que enunciamos a continuación.

Proposición. Un espacio topológico $(X, \tau)$ es Hausdorff si, y solo si, la diagonal $\Delta = \{ (x,x) \in X \times X \mid x \in X \}$ es un subconjunto cerrado del producto $X \times X$.

Demostración

Corolario. Sean $f, g : X \to Y$ dos aplicaciones continuas en un espacio $Y$ de Hausdorff. El conjunto de puntos en que ambas coinciden, $\, \{ x \in X \mid f(x) = g(x) \}, $ es un cerrado de $X$.

Demostración

No solo es importante la separación entre puntos, sino también lo es la separación entre cerrados y entre puntos y cerrados.

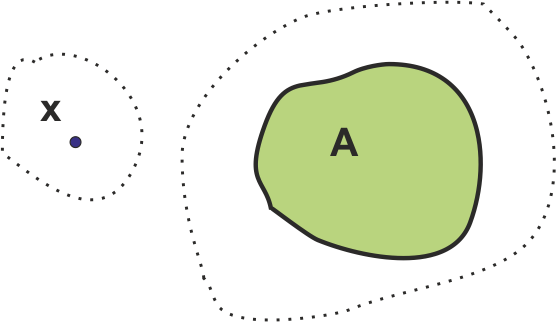
Se dice que un espacio topológico $(X, \tau)$ es $T_3$ si dado un cerrado $A$ y un punto $x \not\in A$, existen abiertos disjuntos que los contienen. Un espacio $T_3$ y Hausdorff se llama espacio regular.

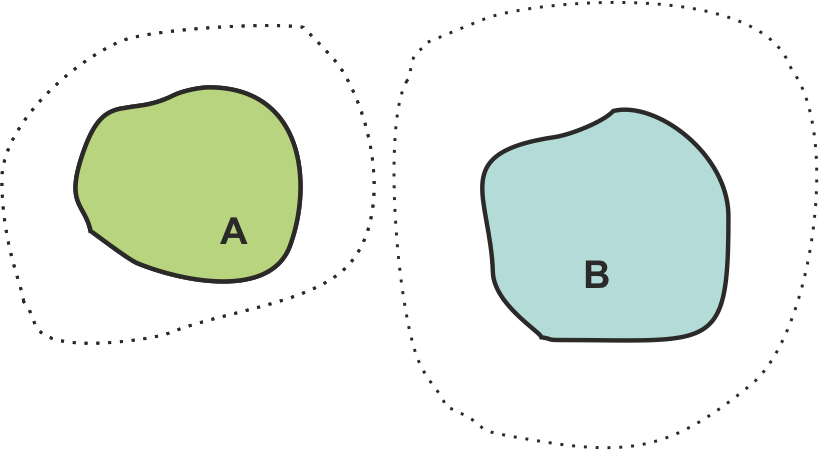
Se dice que un espacio topológico $(X, \tau)$ es $T_4$ si dados dos cerrados disjuntos, $A \cap B = \emptyset$, existen siempre abiertos disjuntos que los contienen. Un espacio $T_4$ y Hausdorff se llama espacio normal.

¿Pero acaso un punto no es siempre cerrado? En los espacios métricos sí, ciertamente, pero no siempre son cerrados. Por ejemplo, si $X$ tiene más de un punto y la topología burda, los puntos no son cerrados. La propiedad Hausdorff implica que los puntos son cerrados, ya que el complementario un punto es abierto.

Los espacios topológicos $(X, \tau)$ cuyos puntos son cerrados se llaman espacios de Fréchet y pueden no ser Hausdorff.

Los espacios métricos son muy buenos en el sentido de las propiedades de separación: las tienen todas. O lo que es lo mismo, son espacios normales.

Proposición. Todo espacio métrico es normal.

Demostración

La propiedad de separación $T_4$ resulta ser equivalente a dos propiedades de extensión importantes: el Lema de Urysohn y el Teorema de Extensión de Tietze. En Topología, los problemas de extensión se refieren a la posibilidad de extender a todo el espacio una función continua definida en un subespacio. Mencionamos ya el problema de extensión al hablar de retractos aquí.

Lema de Urysohn. Un espacio topológico $X$ es $T_4$ si, y solo si, dados dos cerrados disjuntos cualesquiera $A$, $B$, existe una aplicación continua $f: X \to [0, 1]$ tal que $f(A) = 0$, $\,f(B)= 1$.

Demostración.

Teorema de Extensión de Tietze. Un espacio topológico $X$ es $T_4$ si, y solo si, toda aplicación continua definida en un subespacio cerrado $A \subset X$, $\, f : A \to [-a, a]$ tiene una extensión continua a todo el espacio, $\, F: X \to [-a, a]$.

Demostración.

No existe un resultado del tipo del Lema de Urysohn para espacios regulares. Es decir, la propiedad $T_3$ no implica que dado un punto y un cerrado, $x \not\in A$, exista una aplicación que tome el valor $0$ en $x$ y el valor $1$ sobre $A$.

Se dice que un espacio es completamente regular si dado un punto $x$ y un cerrado que no lo contenga, $x \not\in A$, existe una aplicación $f: X \to [0,1]$ tal que $f(x)=0$ y $f(A)=1$. Un espacio Hausdorff y completamente regular se llama un espacio Tychonoff.

Abordemos una última cuestión importante. ¿Qué propiedades de separación de un espacio topológico se conservan cuando se toman subespacios, se hacen productos, se hacen cocientes o, en general, se toman imágenes por aplicaciones continuas?. Es decir, en las construcciones de nuevos espacios a partir de otros ¿qué propiedades heredan los nuevos espacios?

Proposición. 1. Todo subespacio de un espacio Hausdorff es Hausdorff. Todo subespacio de un espacio regular es regular. Todo subespacio cerrado de un espacio normal es normal.

2. El producto de espacios de Hausdorff es de Hausdorff. El producto de espacios regulares es regular. (En cambio, el producto de espacios normales no siempre es normal.)

3. Ninguna propiedad de separación se conserva automáticamente al hacer cocientes.

Demostración