El ejemplo por antonomasia

La Topología es un tipo particular de geometría y los espacios más frecuentes en sus aplicaciones son los subespacios de los espacios ordinarios: recta, plano, espacio tridimensional o de cualquier dimensión superior.

Desde el punto de vista matemático son subconjuntos de n-plas de números reales: $A \subset \mathbb R^n$. Cuando $n$ es 1, 2 o 3, podemos representar $\mathbb R^n$ como los puntos de una recta, un plano o el espacio tridimensional ordinario; el objeto matemático formal, representa así un objeto físico cuyas propiedades y comportamiento tratamos de estudiar.

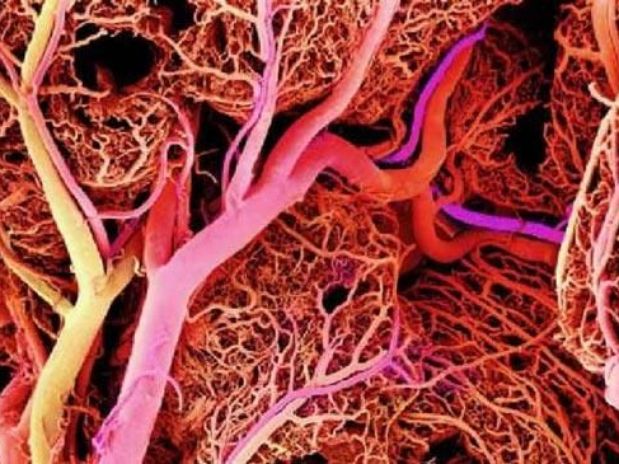
En el conjunto de venas de la figura, la Topología no se interesa por su tamaño, longitud o grosor, sino por las conexiones entre ellas, el número de bifurcaciones, los circuitos que puedan formar, etc. En una figura porosa como la de la esponja estaremos interesados en las cavidades que pueda tener, si son cerradas, aisladas, o las conexiones que haya entre ellas. En la triple anilla contamos el número de agujeros, tres si es maciza pero si es hueca el interior también es un agujero aunque de distinta "dimensión" que los otros tres. Esas son algunas de las cuestiones que estudia la Topología.

La Topología no se interesa por todas las posibles propiedades de un objeto, solo aquellas que se conservan cuando se deforma sin roturas, ni costuras. Todos los subconjuntos que se obtienen deformando uno en otro comparten las propiedades que queremos estudiar. Se ha convertido en un tópico decir que un topólogo es una persona que no distingue entre una taza y un donut. En efecto, la forma de una taza se puede deformar hasta obtener la forma de un donut sin romperla ni pegar partes que estuvieran separadas:

Animación perteneciente a Rio Rancho Math Camp Méjico.

De hecho, el ejemplo de la taza y el donut no es del todo representativo. Realmente, no son las deformaciones lo que determina que dos objetos sean topológicamente equivalentes, sino los homeomorfismos. Dos objetos $X$ y $Y$ son homeomorfos si existe una biyección entre ellos $$ f: X \longrightarrow Y $$ tal que tanto $f$ como su inversa $f^{-1}$ sean continuas; estas aplicaciones se llaman homeomorfismos. Si dos espacios son homeomorfos comparten todas sus propiedades topológicas.

Por ejemplo, desde el punto de vista de la Topología, el intervalo $(-1,1) \subset \mathbb R$ es equivalente a todo $\mathbb R$. En efecto $$ f: (-1,1) \longrightarrow \mathbb R, \qquad f(t) = \tan{\pi t/2} $$

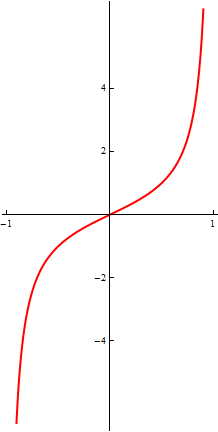
es una aplicación biyectiva, lo que viene a decir que el intervalo y la recta tienen el mismo "número" de puntos; además $f$ es continua y su inversa también es continua. Es esto lo que nos hace identificar los dos objetos en Topología. Así, por ejemplo, que el que un objeto sea acotado en $\mathbb R^n$ no es una propiedad topológica: el intervalo $(-1,1)$ es acotado y todo $\mathbb R$ no lo es.

Ahora bien, dado $A \subset \mathbb R^n$ ¿cómo se consigue aislar las propiedades que nos interesan del resto de propiedades, en particular de la distancia y de la dimensión $n$? Lo vamos a conseguir tomando como espacio topológico el conjunto $A\subset \mathbb R^n$ y, junto con él, el conjunto de uniones de bolas $$ B_d(x,r) = \{ y \in \mathbb R^n, \; d(x,y) < r \}, \quad x=(x_1, \dots, x_n), \quad y=(y_1, \dots, y_n) \in A $$ con centro los puntos $x \in A$ y radio cualquier real positivo $r \in \mathbb R^n$. Aquí $d$ es la distancia usual de $\mathbb R^n$: $$ d(x,y) = \sqrt{(x_1 - y_1)^2 + \dots + (x_n - y_n)^2} $$ Llamaremos abiertos a los conjuntos uniones de bolas.

Cualquier propiedad topológica tendrá que basarse exclusivamente en el conjunto $A$ y en sus abiertos. No es evidente cuales son exactamente estas propiedades, pero pronto lo iremos viendo. De momento observemos que los abiertos los podemos obtener también como unión de conjuntos que no son bolas; por ejemplo, cuadraditos, rombos, etc. Además, si multiplicamos todas las distancias entre dos puntos por un número fijo, los abiertos continúan siendo los mismos. Esto ya nos indica que los abiertos tienen más que ver con una idea genérica de cercanía, o vecindad, que con la distancia $d$ concreta con la que medimos esta cercanía. De momento con eso nos bastará.